[IQA #5] Calculating the distance between Fovea/OD to its respective edges

In the last post, we have described the strategy given to adapt a dataset, in order to detect Fovea in retinal images, using a YOLO-based model. With that, the next step was to find the distance from the Fovea/Macular center to the Temporal Edge. At this point, I will be assuming that every reader knows the retinal structures important to this project.

Prior to that, we had already found the distance from the Optic Disc to the Nasal Edge, by running horizontally, from the OD corner to its closest edge on the binarized retinal image. We did also perform the same kind of operation for the Fovea, until we noticed that not on all the images the Fovea and Optic Disc were approximately horizontally aligned, some images seemed to be angled, which came into consideration.

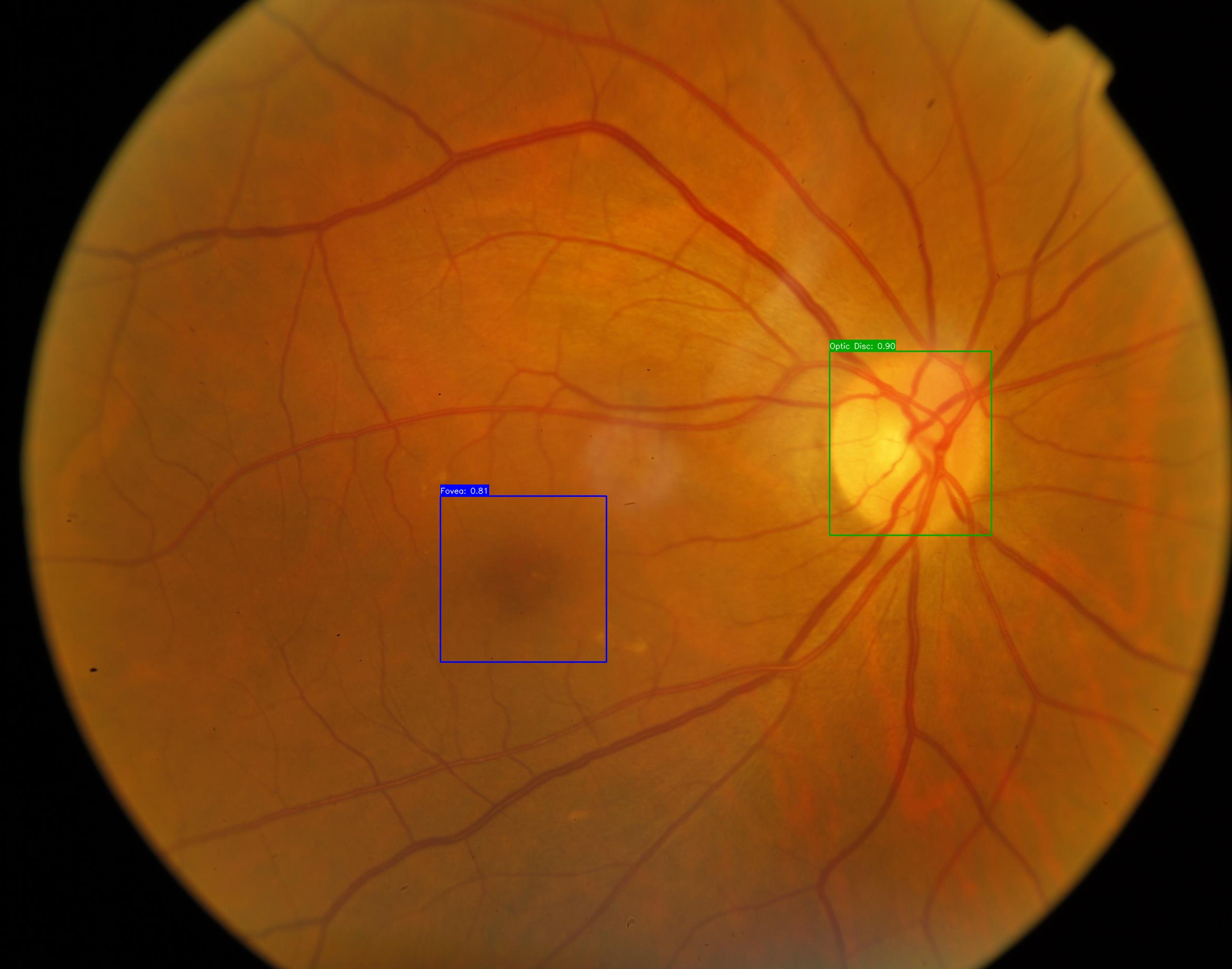High angle between Fovea and Optic Disc

Some works state that there is a small horizontal angle between the two structures, but on some images the angle was just too high, which made us start thinking that only walking horizontally, from the OD corner or the Macular Center to the closest edges would not be the best approach to detect this distance. By doing so, we could be walking towards another area, not of our interest, on the temporal/nasal edges.

Our idea to deviate from the problem

For now, we are going to use some geometry concepts. Given the problem stated on the introduction and assuming that we are only working with the Optic Disc distance to the Nasal edge for now, we want to find the most correct Nasal Edge point in relation to the Optic Disc, in order to measure the actual distance between the two structures.

To do so, we take the line that passes through the OD Center and the Fovea Center, and define the center of the OD as \((c_x, c_y)\). In order to get the nasal unit vector, that passes through both points, we do:

\[\vec{U} = \frac{OD_{Center} - Fovea_{Center}}{||OD_{Center} - Fovea_{Center}||}\]

Assume now that the Optic Disc is an elypse. With that, given that we know the semi-axis \(a\) and \(b\), given by our YOLO model as width and height of the OD, we can find all points in its borders by using the parametric equations:

\[x = c_x + a \times cos\ \theta\] \[y = c_y + b \times sen\ \theta\]

The only thing left to do is find the \(\theta\) angle, in order to find the point we want. To do so, we generate \(1000\) equally spaced points on the interval \([0, 2\pi]\), and choose the point that maximizes the projection on the unit vector \(\vec{U}\).

def getNasalPointOnOD(odCenter, width, height, nasalUnitVector):
    cx, cy = odCenter
    ux, uy = nasalUnitVector

    ts = np.linspace(0, 2*np.pi, 1000)
    xs = (width/2) * np.cos(ts)
    ys = (height/2) * np.sin(ts)

    projections = xs * ux + ys * uy

    idx = np.argmax(projections)

    x_nasal = cx + xs[idx]
    y_nasal = cy + ys[idx]

    return x_nasal, y_nasal

All of this was done in order to find the Optic Disc’s closest point to the Nasal Edge. This is important, instead of just taking the right/leftmost point or just some other point on the bounding box, that could not really be on the Optic Disc. For this work, we will call this point the Nasal Point. The nasal vector and nasal point can be visualized on the following image:

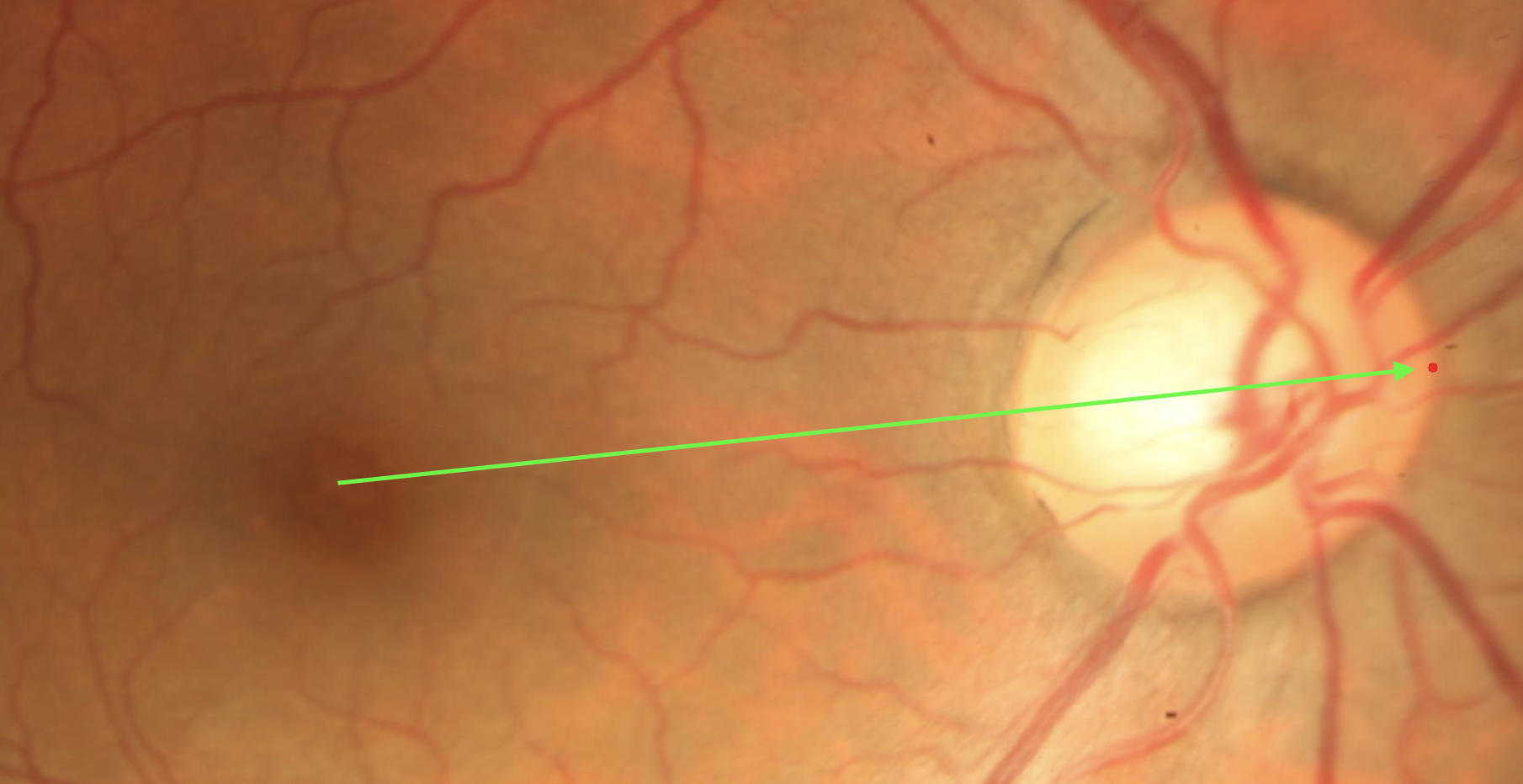Nasal Vector and Nasal Point highlighted

Calculating the distance

At this moment, we already have the Nasal Point and we just need to find the actual distance from this point to the Nasal Edge. Notice that, for the Fovea we do not need to calculate a new point, since we want the distance from its center to the Temporal Edge, so we can get an approximation of this point only by using the YOLO prediction center coordinates.

To calculate this distance, we can use the same algorithm for both the OD-Nasal Edge distance and the Fovea-Temporal Edge distance, just inverting the Unit vector \(\vec{U}\) given before. We use the following procedure:

1. Binarize the retinal image, to isolate the retina from the background

2. Extract the retinal contours using OpenCV cv2.findContours() function.

3. Transform the contours into a shapely library polygon

4. Create a line, extending the unit vector \(\vec{U}\)

5. Get the point where the line intersects the contour

6. Calculate the distance between this point and the retinal point of interest

You can see that this whole procedure gets really easy by using OpenCV and Shapely libraries.

With all that done, we finished detecting the distance between Fovea and Optic Disc, by using the retinal objects geometrical properties. Now, me and my advisor are in touch with the ophthalmologist responsible for the BRSet dataset, in order to check if this way of finding the Nasal and Temporal Edges distance to the Optic Disc and Fovea, respectivelly, is the correct way of dealing with this problem.

Next Steps

From what we have seen so far, the only next thing to do, beyonds reviewing what was discussed on this post, would be assessing the visibility for the inferior and superior arcades. But considering the [Extra 1] post, we will be running a statistical analysis on BRSet, in order to detect all the images that may be mislabeled, by only running the first two Image Field properties that should be checked on adequate images. Also, this week we will start to write an Undergraduate research paper, to publish on SIBGRAPI 2025, a conference on Computer Vision that will be held in Salvador, Bahia. With that said, since the third Image Field property seems to be a totally different approach for solving, and won’t be performed in time for the paper. We will continue to work on top of this, though.

• Understanding and studying the problem
• Choosing dataset
  • Preprocessing data
• Define training baseline
• Applying YOLO to detect Optic Disc (OD)
  • Obtaining the disc diameter (DD)
  • Obtaining distance from the OD to the Nasal Edge
• Detect Macular Center
  • Obtaining the distance from the Macular Center to the Temporal Edge
• Run statistical analysis on BRSet annotations
• Paper submission for SIBGRAPI
• Assessing visibility for the inferior and superior arcades

This post is used as a research checkpoint for the image quality assessment research on retinal fundus images, supervised by professor Nina S. T. Hirata, from the Institute of Mathematics and Statistics at the University of São Paulo (IME USP). The project is supported by USP/MCTI/Softex/Motorola.